Alternate url for this page:
http://tinyurl.com/mathematicianscope

What Is A Historyscope?

Westerners are not only known as history ignoramuses, but double dumbass history ignoramuses when it comes to mathematicians and mathematics history. Since I'm the one-and-only Historyscoper (tm), let me quickly bring you up to speed before you dive into my Master Historyscope.

Mathematics itself is eternal, hence there can be no history of it as such, only a history of mathematicians and the publications of their discoveries and creations.

About 1822 B.C.E. the Babylonian clay tablet Plimpton 322 Table (-1762?) in Larsa, Iraq (modern-day Tell as-senkereh) shows an advanced knowledge of trigonometry incl. Pythagorean triples; they don't base their math on angles but on sexagesimal arithmetic, giving exact results.

About 600 B.C.E. Thales of Miletus (-624 to -547) becomes what was regarded by Aristotle as the first philosopher; "Western philosophy begins with Thales" (Bertrand Russell); he becomes the first to break with religion and attempt to explain Nature without resorting to mythology, becoming known as "the Father of Science"; he regards water as the arche (source of all things), and leaves Thales' Theory of Geometry and Thales' Intercept Theorem, becoming the first true mathematician who discovers a mathematical theorem and uses deductive reasoning to derive four corollaries.

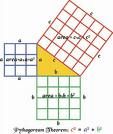
Shut your pi hole and do your math homework? In 530 B.C.E. after traveling to Egypt and learning the doctrines of the Egyptian priests, Greek Ionian philosopher Pythagoras (-580 to -497) is driven from Samos by tyrant Polycrates, and founds his mystical philosophical sect in Italy's Toe City Croton (Crotona), teaching reincarnation, numerology, and dietary restrictions (no beans), and gaining the support of superstar athlete Milo of Croton after claiming to be a reincarnation of Trojan War soldier Euphorbus; although he leaves no writings, his school discovers the Pythagorean Theorem and raises math to a science, considering Number to be the ultimate principle of the Universe, and believing the Earth to be a globe revolving with the planets (incl. the Sun) around a central fire, separated from each other by intervals corresponding to the harmonic lengths of strings, which play the "music (harmony) of the spheres"; Pythagoreans don't eat beans because they make bad music?

About 450 B.C.E. Greek Pythagorean philosopher Hippasus of Metapontum (b. -530) dies after discovering the irrational numbers; the gods drown him at sea for divulging his discovery?

About 430 B.C.E. Greek sophist Hippias of Elis discovers the mathematical Quadratix of Hippias (Dinostratus), used for angle trisection.

In 427 B.C.E. the Hindu astronomical Siddhantas (Sansk. "Doctrine/Tradition") begin to be compiled, containing the Hindu numerals and zero.

About 300 B.C.E. Greek mathematiciain Euclid of Alexandria (-325 to -265) pioneers deductive mathematics, and proves the infinitude of the prime numbers, providing the first examples of formal mathematical proofs and algorithms. In -295 he pub. Optica, the first text on geometrical optics. He dies leaving his 13-vol. masterpiece Elements [of Geometry] - and two Alexandrian Compasses in the garage? "There is no royal road to geometry."

In 260 B.C.E. Syracuse, Sicily-born Greek scientist-engineer-mathematician Archimedes (-287 to -212) discovers the law of buoyancy in his bath, shouting "Eureka!", going on to develop the principles of the lever, compound pulley, and other simple machines before being appointed to defend Syracuse from the Romans, creating defensive engineering marvels incl. giant ship-snatching levers, the catapult (600 ft. range, which can be varied as the ships close in), and a mirror device that sets Roman ships ablaze (Greek Fire), all of which make the Romans think of him as a sorcerer. Too bad, in -212 Syracuse is finally captured and sacked by the Romans under Gen. Marcus Claudius Marcellus, and turned into their govt. seat in Sicily; Archimedes is killed in Syracuse by a Roman soldier as he is drawing circles in the sand at the beach and telling him "Don't disturb my circles" (Noli tangere circulos meos). "Dos moi pou sto, kai kino ten gen" (Give me a place to stand, and I will move the Earth).

About 200 B.C.E. Egyptian-born Greek big brain Eratosthenes of Cyrene (-276 to -194) (head librarian of the Library of Alexandria) determines the circumference of the Earth by measuring noon Sun angles in wells at Syene (Aswan) and Alexandria, coming within 50 mi. of the correct value (approx. 25K mi.), suggesting that the Sun moves around the Earth; he also measures the obliquity of the ecliptic with an error of 7 min. of arc, and maps the course of the Nile River; the southernmost point of Africa is considered the Horn of Africa, taking the Greeks and Romans until the 1st cent. C.E. to discover SE Africa; it takes until 1670 C.E. for Christian Europe to catch back up? He also describes the Sieve of Eratosthenes for finding all prime numbers up to a given limit.

In 70 C.E. Greek mathematician-engineer Heron (Hero) of Alexandria (b. 10) dies, leaving Mechanics and Optics, describing the principle of the shortest path of light, the Babylonian method for computing square roots, and Heron's Formula for finding the area of a triangle from its sides, also the design of the first vending machine, which delivers holy water for a coin; Pneumatics, describing Heron's Steam Engine (Aeolipile), with two jets that makes it rotate on its axis, a wind wheel that operates an organ (the first wind-powered machine?), a water pump for fire engines, and the syringe - put that all together and see what kind of party you can throw?

In 168 Egyptian-born Greek mathematician-astronomer Claudius Ptolemy (90-168) dies in Alexandria, Egypt, leaving Almagest (Arab. "Great Compilation) (original title "Astronomical System"), a 13-vol. system of mathematical astronomy placing the Earth at the center of a static Universe, which is accepted by both the Christian and Muslim worlds until the Christian Renaissance; he also leaves Geography, incl. a map of the known world with coordinates given, and The Tetrabiblos, a comprehensive work on astrology.

About 284 Greek mathematician ("Father of Algebra") Diophantus of Alexandria (b. 200) dies, leaving Arithmetica, founding the study of Diophantine equations.

In the 4th cent. (3rd?) (5th?) Chinese mathematician Sun Tzu (Sun Zi) flourishes, leaving Sun Tzu Suan Ching (Sun Tzu's Calculation Classic), containing the how-many-eggs-in-my-basket Chinese Remainder Theorem.

In Mar. 415 after Alexandrian bishop (since 412) (St.) Cyril of Alexandria (376-444) expels the Jews from Alexandria, Greek mathematician-astronomer-philosopher Hypatia of Alexandria (b. 370), the Neoplatonist librarian of Alexandria, who supports Orestes, pagan prefect of Alexandria for opposing persecution of pagans and Jews is jumped in her chariot, stripped naked, and dragged through the streets to the newly-depaganized Caesareum Church, and murdered by a mob of Coptic Christian monks (from Nitria?) led by Peter (working for Archbishop Cyril under the influence of Pulcheria), ending the Hellenistic Age; her skin is scraped off with sharpened oyster shells and she is set on fire while still alive?; the first burning by Christians of a witch?; meanwhile St. Augustine writes "The true image of the Hebrew is Judas Iscariot, who sells the Lord for silver. The Jew can never understand the Scriptures and forever will bear the guilt for the death of Jesus."

In 500 Chinese mathematician Zu Chongzhi (b. 429) dies after calculating pi as between 3.1415926 and 3.1415927, which isn't bested for 8 cents.

In 632 Arab madass warlord prophet Muhammad (570-632) died after creating a new monotheistic religion crossing Judaism, Christianity, and uniquely Arab Allah (Moon god?) worship and ethnically cleansing the Arabian Peninsula, after which his followers launched a takeover attempt of the whole world, starting with Persia, Syria, Egypt, and the Holy Land, which they conquered by 642. The Muslim conquest of Europe sputtered in 732 when they were thrown out of France by Christian hero Charles Martel the Hammer (686-741), grandfather of Charlemagne (742-814). The Great Jihad is still theoretically on today since Allah's commands are set in stone, it's just that the great majority of modern Muslims are pikers who are satisfied with holding past gains. Too bad, Muhammad's infallible Quran combined with his personal example gave divine authority to the most retro social-moral system of the Middle Ages, incl. polygamy, slavery, male supremacy, and subjection of believers in other religions, maybe he was right and a man's testimony is worth that of two women, like it takes two women co-stars to substitute for a male star, like Geena Davis and Susan Surandon in "Thelma and Louise", I now pronounce you husband and wives, Brad Pitt may kiss the brides. In conquering the Zoroastrian Persians, Alexandrian Egyptians, and Byzantine cities, the Muslims captured a number of ancient Greek mss. on Science and Technology, and translated them into Arabic, launching Muslim Science, check out the one-sided Islam history ignoramus Ben Kingsley vids and get back with me about the whopping total of two Muslim Nobel Prize winners for Science out of a pop. 1.x billion, compared to only two Jews, one cripple, and one black. Actually, a total of three Nobels for intellectual (non-political) categories, one for every 450M Muslims alive today, compared to 169 for Jews, one for every 89K, that's a ratio of 5K. Christians fall in the middle. What happened? For Christians, it was the rise of the Roman Catholic Church and its suppression of all free thought that caused it to hold back the rise of Science and stink itself up because all works of ancient pagans, incl. Greek and Roman scientists were considered works of the Devil and banned, like throwing the baby out with the bathwater. Ironically, the Church even suppressed other Christians, particularly those who wanted the Bible alone to be their authority, not Church synods (they later split off permanently as the Protestants starting in 1517). The Muslims, on the other hand, went on for centuries without Science like them, but finally created an elite cadre in Spain (Al-Andalus) and another in Mesopotamia at the House of Wisdom in Baghdad (830) funded by the caliphs, who translated and studied the captured wisdom of da ancient infidels, the land that time forgot, enjoy the scenery just don't upset the natives, and actually advanced Science a bit, about to the modern pre-calculus high school level, no, the 5th grader level, starting with Abu Yusuf Ya'qub ibn Ishaq al-Kindi (801-73) (AKA Alkindus) in Baghdad, who supervised the translation project and introduced Indian numerals to the Islamic world, which made their way to the Christian world and were called Arabic numerals. He stole them from Hindu mathematician Bhaskara I (600-80), who in 629 wrote a verse commentary to the "Aryabhatiya" (499), first using the decimal number system and making it known to Indian scholars. The 499 work was written by Hindu superbrain Aryabhata (476-550), who advanced the theory that the Earth rotates on its axis, gave the correct explanation for eclipses of the Sun and Moon, the value of pi as 3.1416, and solved the quadratic equation with the first known use of algebra, with the soundbyte "The Moon consists of water, the Sun of fire, the Earth of earth, and the Earth's shadow of darkness. The Moon obscures the Sun and the great shadow of the Earth obscures the Moon." Now that the scholars had their Kindles, they ramped things up between their quintuple daily prayer breaks, with Muhammad al-Khwarizmi (780-850) developing algebra (Arabic for restoration), Abu Bakr Muhammad al-Razi (865-925) ("the Islamic Hippocrates") et al. developing medicine and alchemy (Arabic for art of transformation) (the start of chemistry), Alhazen (Abu Ali al-Hasan ibn al-Hasan ibn al-Haytham) (965-1038) of Egypt (who tried to lay low from the caliphs by feigning madness) founding modern optics, and Avicenna (Ibn Sina) (980-1037) of Persia becoming their best all-around raghead brain man. Too bad, it's pretty hard to engage in a laborious lab research project when you have to stop and pray 1-2-3-4-5 times a day to the non-existent Blaalah while Islamic police hold scimitars over your necks, and since religious dictators control society, any and every advance you make is immediately subjected to scrupulous examination for potential heresy, which they call Bid'ah ("innovation"), plus why aren't you out there with everybody else, Abdul, killing infidels for Allah, what are you, a draft evader? Actually, the general Muslim pop. always hated and feared Muslim scientists, as they do now, and they could only do it under the protection of a powerful ruler. As De Lacy O'Leary (1872-1957) put it: "Islam generally had its own wise men, men learned in jurisprudence, tradition, and Qur'an. These were universally respected with ungrudging esteem, such as was never rendered to the scientists who were only tolerated because they were under state protection. It very much tempers our estimate of Arabic learning to remember that scientific and philosophical scholarship was confined to one privileged coterie." Until the West began taking over in the Renaissance, both the Islamic and Christian worlds accepted Ptolemy's 2nd cent. C.E. Almagest ("Great Compilation") that claimed that the Earth is the center of the Universe and everything else revolves around it, let's make a muscle, make a difference, and flex for MDA, they were neck-in-neck in astronomical stupidity while claiming to have pipelines to God. Speaking of Islam killing not incubating Science, around 1100 Persian Sunni Sufi mystic theologian Abu Hamid Muhammad al-Ghazali (1058-1111) started a reaction against ancient Greek and Roman learning, launching the theory of Occasionalism, to the effect that all cause and effect is determined not by scientific laws but by Allah and his angels, with the soundbyte "A clumsy and stupid person must be kept away from the seashore, not the proficient swimmer, and a child must be prevented from handling a snake, not the skilled snake-charmer", along with the soundbyte: "The gates of ijtihad (rational debate) in Islam are now closed", meaning that perfection had been reached in both social and spiritual philosophy, hence the conservatives rule and the rationalists are out, causing an Islamic theocracy to be built up which regarded the very concept of scientific laws as an affront to Allah and an infringement of his freedom to act, after which Islam became kaput as an engine of science, and only kept a few engineers around to build butt bombs. Hence, Islam had its chance to prove to the world that it was the leader in science and technology who would turn Earth into a paradise, and blew it bigtime, forever proving it to be the opposite, watch that pothole it might contain an IED, which to be fair puts it on a par with the horrible mean Roman Catholic Church, let's rack 'em up, it seems like the Devil takes over all big organizations after enough time, which is why the little guy has to know who's at the top, God or the Devil, and bypass the organization as necessary to get to the real dude. Not that it's all the Muslims' fault. The House of Wisdom was destroyed by the Mongols of Hulagu Khan in 1258, after which the waters of the Tigris River ran black for 6 mo. from all the ink from the ruined books. In the 1420s brain man and future Persian Mongol Timurid sultan (1447-9) Ulugh Beg (1393-1449) (grandson of Tamerlane) founded the Samarkand (Ulugh Beg) Observatory, which had instruments to measure precise star positions, becoming the last great Muslim observatory, compiling books of trigonometric tables of sine and tangent values accurate to 8 decimal places; despite science being all-but dead in the Muslim World, thanks to the headlock of the Church, Muslim science remained far ahead of Christendom until about 1600, and I think by now we know that no Bible-thumping religion can claim credit, only scientists who braved the Bible-thumpers, which became easier to do in Christendom because Jeezy never said kill infidels like Muhammad did. In summary, as Pakistani nuclear physicist Pervez Amirali Hoodbhoy (1950-) recently put it, for the last 700 years Islam and Science have "parted ways", and even today Muslims tend to go into engineering rather than science since it strains their belief system less.

In 820 Euclid's Elements becomes the first ancient mathematics trs. from Greek into Arabic by the House of Wisdom in Baghdad; meanwhile about this year Persian Muslim House of Wisdom mathematician Muhammad Ibn Musa al-Khwarizmi (780-850) pub. Al-kitab al-mukhtasar fi hisab al-gabr wa'l-muqabala (The Compendious Book on Calculation by Completion and Balancing), which is tr. into Latin in 1145 by Robert of Chester under the title Liber algebrae et almucabola, coining the terms "algebra" (Arab. "reuniting", "restoration"), "algorithm, and "x" for the uknown quantity, along with "sine" after mistranslating the Arabic word "jb" as bay or inlet, which becomes sinus in Latin.

About 900 Indian mathematician Sridhara (870-930) discovers the power of the zero (suro) ("seed") ("circle") (the Sun divinity incarnate?) - are you the fat one in the family?

In 1066 Indian mathematician-astronomer Sripati (b. 1019) dies, leaving Dhikotidakarana (1039), a book on solar and lunar eclipses, and Dhruvamanasa (1056) on calculation of planetary longitudes, eclipses, and planetary transits; he also leaves Siddhantasekhara, about arithmetic, algebra, and calculations on the sphere, and Jyotisaratnamala, Jatakapaddhati (Sripatipaddhatih), and Daivajnavallabha, books on astrology.

In 1202 Italian mathematician Leonardo (OG "lion bold") Fibonacci (Filius Bonaccii) (Leonardo Pisano) (Leonardo da Pisa) (1170-1250) pub. Liber Abaci (Book of the Abacus), introducing the Hindu-Arabic place-value system and Arabic numerals to Europe, and discussing the Fibonacci Sequence ("How many pairs of rabbits can be produced from a single pair in a year's time?"); forever after science and sex are romantically intertwined in Euro minds? In 1220 he pub. Practica Geometriae, first applying algebra to prove geometrical theorems. In 1225 he pub. two works contributing to the solution of equations of the first and second degree, and competes in a math tournament with John of Palermo supervised by HRE Frederick II.

In 1222 Jordanus Nemorarius (Jordanus de Nemore) (Giordano of Nemi) becomes gen. #2 of the Dominican Order, going on to dabble in science, using Hindu numerals and doing algebra with letters, writing Elementa Super Demonstrationem Ponderis, discussing the component of gravity along a trajectory, and expounding Jordanus' Axiom, that a force that can raise weight W to height H can raise weight K*W to height H/K. He also writes De Ratione Ponderis, discussing statical moments (the product of force and a lever arm), and The School of Jordanus, discussing the theory of virtual displacements.

In 1229 Morrocan Muslim scholar Hasan al-Marraqushi pub. tables of sines, versed sines, arc sines, and arc cotangents for each degree.

In 1247 Chinese scholar Qin Jiushao writes Shushu Jiuzhang, which contains the phrase "in all old books we find empty places", referring to the zero.

About 1250 Persian Muslim mathematician Nasir ud-Din al-Tusi (1201-74) of Tus, Khorasan pub. the first treatise treating trigonometry as its own subject rather than a part of astronomy; it takes the Euros two cents. until Regiomontanus (1436-76) to equal it.

In 1292 English scientist-friar Roger Bacon (b. 1214) dies near Oxford, and is buried in Grey Friars' Church, leaving the soundbytes: "Mathematics is the gate and key of the sciences... Neglect of mathematics works injury to all knowledge, since he who is ignorant of it cannot know the other sciences of the things of this world"; "If in other sciences we should arrive at certainty without doubt and truth without error, it behooves us to place the foundations of knowledge in mathematics."

In 1299 after lobbying by abacists, a law is passed in Florence against using "newfangled figures" (Hindu numerals, the zero, decimals) to do accounting; Hindu numerals don't replace Roman numerals until the 16th cent.

In 1303 Chinese Yuan Dynasty mathematician Chu Shih-Chieh (Zhu Zhijie) (1249-1314) writes Szu-yuen Yu-chien (The Jade Mirror of the Four Unknowns/Origins) (3 vols.), 288 algebra problems incl. quadratic and cubic equations, series and progressions, describing Pascal's Triangle; it covers the Tian yuan shu (Method of the heavenly element/celestial unknosn) system for solving polynomial equations.

In 1343 French mathematician Jean de Meurs pub. Quadripartitum Numerorum (Four-fold Division of Numbers), a treatise on mathematics, mechanics and music.

In 1344 French Jewish philosopher Gersonides (b. 1288) dies in Perpignan, France, leaving De Numeris Harmonicis (Concerning the Harmony of Numbers), a commentary on the first five books of Euclid.

In 1471 German astronomer Regiomontanus (Johannes Muller von Konigsberg) (Johannes Müller von Königsberg) (1436-76), pupil of Austrian astronomer Georg von Puerbach (Purbach) (1423-61) sets up the Nuremberg Observatory, the first European observatory. In Jan. 1472 he measures the angular diam. of comets, and helps pub. Puerbach's Theoricae Novae Planetarum, which features diagrams of the system of solid spheres. In 1457 Puerbach pub. Pro Pluribus Annis in Vienna, becoming the first printed almanac. In 1473 Regiomontanus pub. Ephemerides ab Anno, an almanac for 1475-1505, used by Columbus. In 1474 he pioneers lunar nautical navigation. In 1475 he is called to Rome by Pope Sixtus IV to help reform the pokey Julian Calendar, which is now eight days behind, with the vernal equinox falling on Mar. 12 instead of Mar. 20; too bad, he dies of the plague next year before doing it. He leaves De Triangulus, which becomes the std. textbook on trigonometry.

In 1505 Italian mathematician Scipione del Ferro (1465-1526) partially solves the cubic equation, obtaining the full solution in 1520.

In 1537 Portuguese mathematician Pedro Nunes (Petrus Nonius) (1502-78) pub. Treatise in Defense of the Maritime Chart, the first discussion of the Rhumb line, a path with constant bearing relative to true north (loxodrome). In 1542 he invents the Nonius, predecessor of the Vernier scale.

In 1537 Italian mathematician Niccolo (Niccolò) Fontana Tartaglia (Ital. "stammerer") (1500-57) pub. Nova Scientia (A New Science), which discusses projectile trajectory and the motion of heavy bodies, proposing Tartaglia's Theorem, that the trajectory of a projectile is a curved line, and that a projectile fired at an elevation of 45 deg. will travel the farthest, founding the science of Ballistics - heavy balls as a cure for stammering? In 1556-60 he pub. General Trattato di Numeri et Misure in Venice, containing Tartaglia's Formula for the volume of a tetrahedron, becoming the #1 treatise on arithmetic in the 16th cent. Too bad, he is tricked by Italian mathematician Gerolamo (Girolamo) (Geronimo) Cardano (1501-76) into revealing his solution to the cubic equation on the promise of keeping it secret, only to be betrayed, causing a running feud with Cardano and his student Ludovico Ferrari (1522-65). Cardano goes on to pub. solutions to the cubic and quartic equation, acknowledge the existence of imaginary numbers, help found mathematical probability, introducing binomial coefficients and the binomial theorem, pub. "De Proportinubus" in 1570, describing hypocycloids, and invent the combination lock, gimbal, universal joint, and biconvex lens.

In 1567 Italian mathematician Fabrizio Mordente (1532-1608) pub. the first description of the Proportional (Military) Compass (Sector).

In 1570 Sir Henry Billingsley ((-1606) pub. The Elements of Geometrie of the Most Ancient Philosopher Euclide of Megara, the first English trans. of "Euclid's Elements"; printed in folio by John Day, incl. several 3-D fold-up diagrams illustrating solid geometry; the preface by mathematicisn-astrologer John Dee (1527-1609) extols the virtues of mathematics, becoming more important than Francis Bacon's "The Advancement of Learning" (1605).

In 1571 English mathematician Leonard Digges (1520-59) (father of astronomer Thomas Digges) invents the Theodolite for surveying.

In 1571 French atty. and part-time mathematician Francois Viete (Viète) (Franciscus Vieta), Seigneur de la Bigotiere (Bigotière) (1540-1603) pub. his first mathematical work Francisci Vietœi universalium inspectionum ad canonem mathematicum liber singularis, a book of trigonometry, containing many sine and cosine formulas, and making use of decimal fractions; he then gets into codebreaking for Henry III and Henry IV during the Wars of Religion while working on his Analytical Art (New Algebra) (Species Logistic) (The Logic of Species), becoming the first to use letters as parameters in algebraic equations, discovering Vieta's formulas relating the coefficients of a polynomial to sums and products of its roots; in 1593 he pub. the first infinite product in an expression for pi as 2 x 2/sqr(2+sqr(2+sqr((2+sqr((2+sqr(2+)...); in modern times the technique of Vieta Jumping is developed to solve mathematical olympiad problems; Rene Descartes builds on Viete's work.

In 1595 German mathematician Bartholomaeus (Barthelemy) (Bartholomeo) Pitiscus (1561-1613) pub. the Latin work Trigonometria: sive de solutione triangulorum tractatus brevis et perspicuus (5 vols.) in Heidelberg, coining the term "trigonometry", which carries into English (1614) and French (1619) translations; je first borrows, er, uses decimal pits, er, points in his trigonometry tables, which he gets the big idea of using for problems on Earth instead of the heavens.

In 1614 Scottish Protestant mathematician John Napier (Neper) of Merchiston (1550-1617) pub. Description of the Marvelous Canon of Logarithms (Mirifici Logarithmorum Canonis Descriptio), which gives mathematicians and astronomers a new improved method of computation, and uses the decimal point to express decimal fractions.

On Nov. 10-11, 1619 (St. Martin's Day) (night) after joining the Dutch States Army in 1618, La Haye en Touraine, France-born philosopher-mathematician (Roman Catholic) (Rosicrucian) ("Father of Modern Philosophy") Rene (René) Descartes (1596-1650) has divine visions in Neuburg an der Donau, Germany in which he "discovered the foundations of a marvelous science", which later becomes Analytic Geometry, along with his famous dictum "Cogito ergo sum" (Je pense donc je suis), causing him to dedicate his life to the mathematical basis of Nature; in 1620 he leaves the army, returning to the Dutch Repub. in 1628, spending 20 years formulating his philosophical works; in 1637 after the horrific Galileo affair, he pub. Discourse on Method (Discourse on the Method of Rightly Conducting One's Reason and Seeking Truth in the Sciences (Discours de la Methode pour bien Conduire sa Raison, et Chercher le Verite dans les Sciences); an epoch-making work expounding the technique of divide and conquer, containing the three appendices (Qui Sont des Essais de Cete Methode): La Dioptrique, advancing the corpuscular theory of light; Les Meteores: Traite de la Lumiere, on cosmology; and La Geometrie, founding the field of analytic geometry and introducing the concepts of a coordinate plane and a mathematical function. In 1644 he pub. Principia Philosophiae (Principles of Philosophy) in Amsterdam, containing the ultimate philosophy soundbyte "Je pense, donc je suis" ("I think, therefore I am"); too bad, it kowtows to the Roman Catholic 1616 anti-Copernican decree by stating that "I want what I have written to be taken simply as an hypothesis, which is perhaps far removed from the truth"; it declares that all motion is relative, thus the Earth can be considered at rest like the Church dictates, drawing criticism from Newton; also that bodies can act on each other only through contact; famous for its diagrams of vortices in which planets are carried in the whirlpool of subtle matter around the Sun - don't try to fight it, don't try and save me, she's a woman in love? In 1662-4 he posth. pub. Treatise on the World, proposing the Dualistic Model of Reality, mind vs. matter.

In 1621-2 William Oughtred (1574-1660) of England invents the logarithmic scale along with the slide rule, which does multiplication and division by adding and subtracting logarithms - did it hurt? Oughtred also coins the terms "x" for multiplication, "sin" for sine, and "cos" for cosine.

In 1628 French-born Dutch mathematician Albert Gerard (Girard) (1595-1632) first uses brackets and other abbreviations in mathematics, going on to become the first to discuss imaginary numbers (square root of -1), provide an inductive definition for Fibonacci numbers, use the abbrevs. sin, cos, and tan for trig functions, and to state this year that each prime of the form 1 mod 4 is the sum of two squares - the original going Dutch?

In 1630 Richard Delamain (1600-44) of England invents the Circular Slide Rule.

In 1637 French atty. and math dabbler ("Father of Number Theory") Pierre de Fermat (1607-65) conjectures Fermat's Last Theorem (that the Pythagorean Theorem for n greater than 2 is not solvable in integers) in the margin of his copy of Diophantus' Arithmetica, with the famous soundbyte that he "discovered a truly remarkable proof which this margin is too small to contain", launching a massive search for the proof after the Royal Academy of Sciences at Gottingen offers a 100K mark prize to prove it true or false, without takers; Fermat proves it for n=4, Leonhard Euler proves it for n=3, Peter Gustav Lejeune Dirichlet proves it for n=5 and n=14; in 1954 an electronic calculating machine proves it true for n less than 2000; it is finally solved in 1994 by English mathematician Sir Andrew John Wiles (1953-) after seven years locked up by himself, who also proves that all rational semistable elliptic curves are modular.

About 1642 French superbrain mathematician Blaise Pascal (1623-62) designs a calculating machine called the Pascaline, which performs addition and subtraction and can do multiplication and division via repeated you know what - if only he'd also invented electronics, he coulda been a contender? In 1654 French mathematicians Blaise Pascal (1623-62) and Pierre de Fermat (1607-65) pub. the basic laws of Probability Theory; Pascal invents the roulette wheel as a by-product of experiments with perpetual motion.

In 1660 Languedoc-born French mathematician-priest (Jesuit) Antoine de Laloubere (Laloubère) (1600-64) and Arnaldum Colomerium pub. Veterum Geometrica promota in septem de Cycloide Libris et in duobus adjectis Apprendicibus in Toulouse, becoming the first mathematical work on the properties of the helix.

In 1662 English economist Sir William Petty (1623-87) pub. A Treatise of Taxes and Contributions, inventing statistical mathematics.

The year 1666 contains all the Roman numerals MDCLXVI) once; also 1444, 1446, 1464, 1466, 1644, 1646, 1664. In 1666 the Millennium Fever (MF) over the Big Year 1666 stirs mass paranoia in Christendom, the smart money being that all those evil scientists and secular pagans (and the antichrist pope and his papist followers, according to Protestants) are going to be consumed in fire just as the unbelievers were consumed in water in the days of Noah; later, when the disappointment sets in, hope springs eternal in the human breast, so anybody born in this year is suspected of being the Devil or the Antichrist, and Armageddon is at least going to happen in his lifetime, so don't give up the faith?; meanwhile never fear, the Scientists are here, as the Annus Mirabilis of English Cambridge U. man Sir Isaac Newton (1642-1727) begins when the plague causes him to be sent home from Cambridge to his home in Woolsthrope, where the world's most famous apple falls from the tree, revolutionizing Science with the stunning realization that the heavens and the Earth are subject to the same universal laws - one little orb falls from the sky, causing their minds to fall from the divine Heavens into the material world of Earth, and like it? I walk this empty street on the boulevard of broken dreams? Don't let a migraine upset you? As a total rebuff to the Millennium Feverists who say the world is not worth studying (since this is its last year), Isaac Newton goes into a glorious brilliant Rain Man funk in Woolsthorpe and discovers the Integral Calculus (not dental rot but the branch of mathematics) and the Newton's Law of Universal Gravitation (inverse square law), measures the Moon's orbit, and, when not otherwise occupied, buys a glass prism "to try therewith the phenomena of the colours", becoming the first to deduce that the prism splits white light into a spectrum as a result of the different refractive index for each color; sitting under a you know what kind of tree, he observes a you know what falling, and calculates that at a distance of 1 ft. the attraction between two objects is 100 times stronger than at 10 ft., making the super mental leap that the force exerted by the Earth on the apple is the same as that exerted by the Earth on the Moon; "And the same year [1666] I began to think of gravity extending to the orb of the Moon, and having found out how to estimate the force with which a globe revolving within a sphere presses the surface of the sphere, from Kepler's Rule... I deduced that the forces which keep the Planets in their Orbs must [be] reciprocally as the squares of their distances from the centers about which they revolve: and thereby compared the force requisite to keep the Moon in her Orb with the force of gravity at the surface of the earth, and found them answer pretty nearly. All this was in the two plague years of 1665 and 1666, for in those days I was in the prime of my age for invention, and minded Mathematicks and Philosophy more than at any time since" - Isaac Newton, memo in the Portsmouth Collection, 1714; the Newton pippin is later named to commemorate the Big Apple of 1666 - the first modern scientist walks the Earth, and he's white, Anglo-Saxon, and Protestant, but actually not so modern, as he's still got one foot in the past and believes in alchemy and bizarre Bible theories, taking a few years out of his all-important studies to figure out math and physics, in the belief that the Universe is a giant code and he can crack it; his success paradoxically strengthens belief in astrology? Newton's funeral was presided over by "A. (Alexander) Pope".

In 1666 19-y.-o. German polymath superbrain Gottfried Wilhelm von Leibniz (1646-1716) (pr. LIPE-nits), Germany's answer to England's Isaac Newton pub. Disserto de Arte Combinatoria (Discussion of the Combinatorial Art), which formulates the idea that all reasoning and discovery are reducible to an ordered combination of elements, incl. words, numbers, colors, and sounds; contains his suggestion, based on the work of Raymond Lully, that a mathematical language of reasoning should be developed, which is taken up by George Boole et al. In 1672-94 he constructs the Stepped Reckoner, the first calculating machine capable of multiplication and division; the cylindrical crank-operated calculating machine was inspired by a pedometer he saw while on a diplomatic mission to Paris, and he visits London to seek financial backing from the Royal Society, claiming it can calculate trig tables. In 1672 he first describes the mysterious invisible Ether (Aether), so dear to Newtonists; meanwhile in 1672 Isaac Newton announces his discovery of the decomposition of white light into the rainbow, breaking it into spectral colors each with a different index of refraction. In 1679 Leibniz discovers the Binary Number System; he doesn't pub. his findings until 1701.

In 1671 Isaac Newton writes Methodus Fluxionum et Serierum Infinitarum (The Method of Fluxions and Infinite Series), describing the notion of fluxions (time derivatives) and fluents (inverse of fluxions, i.e., integrals); his hesitancy to pub. his secret veapon Calculus until 1736 allows Gottfried Wilhelm von Leibniz to claim prior discovery and get into a cross-Channel pissing contest; actually Leibniz rediscovers the Calculus in 1675, but his prettier notation becomes std.

In 1678 Italian mathematician Giovanni Ceva (1647-1734) pub. the elegant Ceva's Theorem on the division of sides of a triangle.

In May (Aug.?) 1684 celeb Edmund Halley visits Sir Isaac Newton in Cambridge to ask what orbit a body would describe under an inverse-square law of attraction, and Newton replies an ellipse, and that he had proved it years earlier but lost the papers and would rework it and send it to him, which he does in Nov., pub. De Motu Corporum in Gyrum (On the Motion of Revolving Bodies) in Dec., then expanding the work, until in 1687 he pub. his monumental "Principia" at Halley's expense; meanwhile Leibniz pub. his system of the integral and differential calculus independently of Newton, allegedly based on his own work from 1673-6, starting a doowahdiddydiddy credit-seeking race; Newton wins the decision for priority with the great tale of the apple in the plague year of 1666 and his killer theory of gravity, but Leibniz' cooler notation gets adopted by textbook writers.

On July 5, 1687 English #1 superbrain Sir Isaac Newton (1643-1727) pub. Philosophiae Naturalis Principia Mathematica (pr. prin-KIP-ee-ya), founding celestial and terrestrial mechanics with his Three Universal Laws of Motion, proving the inverse square law of gravitation and many other basic results after a bitter feud with Robert Hooke (1635-1703) over priority; the rough ms. is finished on June 20, 1686, but he adds a section on comets with the help of John Flamsteed; the preface acknowledges Edmund Halley, saying "it was through his solicitations that it came to be published."

In 1696 French mathematician Guillaume de L'Hôpital (Hopital) (1661-1704) pub. L'Analyse des Infiniment Petits pour l'Intelligence des Lignes Courbes, the first textbook on infinitesimal calculus, based on lectures by his teacher Johann Bernoulli (1667-1748); it incl. L'Hopital's (L'Hospital's) Rule for solving the indeterminate form 0/0 through repeated differentiation - send it to the differential hospital?

In 1713 Swiss mathematician Jacob Bernoulli (1654-1705) pub. the primitive form of the Law of Large Numbers, that the average of a large number of trials converges to the expected value.

In 1718 French-born mathematician (in London) Abraham de Moivre (1667-1754) pub. The Doctrine of Chances, the first textbook on probability theory, prized by gamblers. In 1830 he pub. Miscellanea Analytica, the first book to use a probability integral with an integrand consisting of the exponential of a negative quadratic; it contains De Moivre's Formula, using complex numbers in trigonometry, bringing it into the realm of analysis.

In 1721 Breslau, Silesian-born German mathematician-philosopher Christian Wolff (1679-1754) of the U. of Halle, a disciple of Gottfried Leibnitz known for ditching Latin for German gives the lecture "On the Practical Philosophy of the Chinese", citing the moral axioms of Confucius as proof that human reason can attain moral truth by its own efforts without Biblical revelation, pissing-off the religious (mainly Pietist) faculty; on July 12, 1723 Wolff gives another lecture comparing Moses, Christ, Mohammad, and Confucius, which attracts 1K students, pissing-off the Pietists, who convince Frederick William I that Wolff's determinism would ruin military discipline, causing him to be banished to Prussia for atheism and fatalism, where he teaches at the U. of Marburg in Hesse-Cassel until 1740, when Frederick II the Great recalls him and makes him a celeb, getting him promoted to chancellor of the U. of Halle in 1743.

In 1730 English mathematician John Hadley (1682-1744) invents the Octant (precursor to the sextant) for sea navigation to determine latitude; Thomas Godfrey (1704-49) of British Am. independently invents it.

On Dec. 5, 1735 28-y.-o. Swiss genius mathematician Leonhard Euler (1707-83) pub. his solution to the Basel Problem, which was first proposed in 1650 by Pietro Mengoli and baffled generations of mathematicians incl. the Bernoullis, making him an instant star; the problem asks for the infinite sum of (1/n^2), which turns out to be pi squared divided by 6. In 1736 Euler solves the Konigsberg (Königsberg) Bridge Problem, and founds the study of Analytical Mechanics. In 1744 he discovers the Calculus of Variations. In 1752 he pub. the Polyhedron Face-Vertex-Edge Formula f+v=e+2 (e.g., f=6, v=8, e=12 for a cube, f=32, v=60, e=90 for a buckyball). In 1768 he proposes that the wavelength of light determines its color.

In 1737 English mathematician Thomas Simpson (1710-61) pub. Treatise of Fluxions, in which he derives Simpson's Rule for numerical approximation of definite integrals, which he gets credit for even though it was used by Galileo's student Bonaventura Cavalieri in 1639, and by Johannes Kepler.

In 1738 Swiss mathematician Daniel Bernoulli (1700-82) pub. Hydrodynamica, announcing Bernoulli's Law, a pressure-velocity (PV) relationship for fluids; he derives Boyle's Law by considering a gas as a collection of atoms which collide with the container wall, but everybody overlooks it until it's rediscovered in 1859 - they still teach all that in Top Gun school?

In 1750 Swiss mathematician Gabriel Cramer (1704-52) pub. Cramer's Rule for solving a system of linear equations with matrices and determinants; too bad, Colin Maclaurin beat him to it in 1748?

In 1758 Dalmatian Jesuit mathematician (in Italy and France) Roger Joseph (Ruggero Giuseppe) Boscovich (1711-87) pub. A Theory of Natural Philosophy Reduced to a Single Law of the Actions Existing in Nature (Theoriam Philosophiae Naturalis Redacta ad Unicam Legem Virium in Natural Existentium), which questions Newtonian action at a distance and pioneers field theory, later influencing Michael Faraday.

In 1758 Lyon, France-born mathematician Jean Etienne (Jean-Étienne) Montucla ((1725-99) pub. Jean Etienne Montucla (1725-99), Histoire des Mathematiques (Mathématiques) (4 vols) (1758-1802); completed by Jeome Lalande; "His first volume covered Greek, Roman, and Eastern traditions, while the second covered geometry, mechanics and optics up to the seventeenth century. Forty years later the second edition began to appear, although the author then died and task of completion fell to Jérôme Lalande. With the help of various colleagues, he completed the third volume and wrote the fourth within four years. The first two volumes covered the same material as before, while the other two handled all aspects of the eighteenth century; the whole encompassed around 3000 pages, including indexes (themselves an excellent feature)... One curious feature of the work, especially in chapters on applied mathematics, is the lack of mathematical symbolism in the text: Montucla and Lalande were often content with a verbal account of the work without entering into symbolic renderings. Of course many basic aspects of the history of mathematics were thus left out." (Ivor Grattan-Guinness)

In 1759 German mathematician Johann Heinrich Lambert (1728-77) pub. Treatise on Optics and Treatise on Perspective, causing the unit of brightness to later be named after him. In 1768 he proves that pi is incommensurable (has no common divisor).

In 1761 English mathematician and Presbyterian minister Thomas Bayes (1701-61) dies, leaving "An Essay Towards Solving a Problem in the Doctrine of Chances", containing Bayes' Theorem, which is read to the Royal Society by Richard Price in 1763; the theorem "is to the theory of probability what Pythagoras' theorem is to geometry" (Sir Harold Jeffreys).

In 1766 German mathematician Johann Daniel Titius (1729-96) discovers a pattern in planetary distances, namely that they are in the proportions 4, 7, 10, 16, 28, 52, 100, 196, which happens to be the series 0, 3, 6, 12, 24, 48, 96, 192 with 4 added to each; in 1772 German astronomer Johann Elert Bode (1747-1826) pub. it for the 1st time, causing it to become known as the Bode (Titius-Bode) Law of Planetary Distances; the discovery of Uranus in 1781 checks with the number 196, and the discovery of the asteroid Ceres (orbiting between Mars and Jupiter) in 1801 checks with the missing number 28, however Neptune (388) and Pluto (722) don't pan out, and the Titillating Bogus Law is dismissed as moose hockey (coincidence).

In 1772 Italian mathematician-astronomer Joseph-Louis Lagrange (Giuseppe Luigi Lagrangia or Lagrancia) (1736-1813) pub. a paper proposing the five Lagrange (Libration) Points (L1 to L5), gravitational parking spaces. In 1788 he introduces Lagrangian Mechanics, which uses the Calculus of Variations.

In 1776 27-y.-o. French mathematician brain man Pierre Simon Laplace (1749-1827) pub. the alluring theory that if we know all of the forces on all objects at any one time, then Da Future can be completely predicted - actions can happen at any time, that's why Newton's Law is here? In 1796 he pub. his Nebular Hypothesis. He goes on to pioneer the Laplace Transform, the Laplacian (Laplace Operator), and Laplace's Equation.

In 1776 French mathematician Jean Baptiste Marie Charles Meusnier de la Place (1754-93) pub. Meusnier's Theorem, that all curves on a surface passing through a given point and having the same tangent line at that point also have the same normal curvature at that one cool bitchin' point; he also discovers the mathematical pretty woman Helicoid, the 3rd known minimal surface.

In 1779 French mathematician Etienne Bezout (Étienne Bézout) (1730-83) pub. Theorie Generale des Equations Algebriques in Paris, which contains material on the Elmination Theory, the symmetrical functions of the roots of an equation, and Bezout's Identity, that the greatest common divisor of natural numbers a and b is ax + by for some integers x and y.

In 1792 French mathematician Baron Gaspard Clair Francois Marie Riche de Prony (1755-1839) begins calculating log and trig tables to 14-29 decimal place accuracy - why didn't he invent the computer first?

In 1794 17-y.-o. Johann Carl Friedrich Gauss (1777-1855), a language student at Caroline College in Brunswick, Germany gets interested in math and takes up the classical problem of constructing regular n-gons, proving that it can't be done when n is a prime number except for 17, 65, 257 and 65,537, causing him to switch next year to the U. of Gottingen, submitting a doctoral thesis in 1798 proving the Fundamental Theorem of Algebra (every possible algebraic equation has a solution), going on to become the Princeps Mathematicorum, the #1 mathematician in da whole wide world - I can win that race?

In 1794 after losing fortune last year in the French Rev., French mathematician Adrien-Marie Legendre (1752-1833) pub. Elements de Geometrie, which becomes a std. textbook for the next 100 years. In 1798 he conjectures the Prime Number Theorem, which isn't proved by Jacques Hadamard and Charles Jean de la Vallee-Poussin until 1896. In 1806 he pub. The Path of Comets, containing the first pub. of the Least-Squares Method, developed by Carl Gauss. In 1811 he discovers and names the Gamma Function. In 1830 he proves Fermat's Last Theorem for the exponent n=5. He goes on to conjecture the Quadratic Reciprocity Law (later proved by Gauss), and discover the Legendre transformation and Legendre polynomials.

In 1799 French mathematician Gaspard Monge (1746-1818) pub. Geometrie Descriptive, which incl. a gen. theory of curvature that is used by Carl Friedrich Gauss, making him the inventor of descriptive geometry (used in technical drawing); in 1807 he pub. Application de l'analyse à la géométrie, à l'usage de l'Ecole impériale polytechnique, causing him to become known as "the Father of Differential Geometry".

In 1799 Scottish mathematician William Wallace (1768-1843) pub. the concept of the Simpson Line, the line through the three closest points to a point on the circumcircle of a triangle; in 1821 he improves the pantograph, inventing the Eidograph.

In the first decade of the 19th cent. Science makes great leaps in the concepts of Thematic Cartography, Statistical Graphing, and Data Visualization; coordinate paper is first used in pub. research (graph of barometric variations) by English industrial chemist Luke Howard (1772-1864), who makes comprehensive recordings of London weather in 1801-41. In 1801 the Pie Chart and Circle Graph is pub. London in "Statistical Breviary" by Scottish engineer-economist William Playfair (1759-1823), who in 1786 pub. "The Commercial and Political Atlas" in London, containing the first Bar Chart. In 1801 William "Strata" Smith (1769-1839) of England pub. "the map that changed the world", the first Geological Map (of England), founding the science of Stratigraphic Geology (Stratigraphy); too bad, the establishment ignores him, his work is plagiarized, and he ends up in debtors' prison.

On Jan. 1, 1801 Italian Theatine monk-astronomer Giuseppe Piazzi (1746-1826) discovers the first asteroid, Ceres, and German rising star mathematician Carl (Karl) Friedrich Gauss (1777-1855) computes its orbit using his new Least-Squares Method, which allows it to be found even after it goes invisible and emerges among a multitude of stars, causing him to be appointed dir. of the Gottingen Observatory for life in 1807. going on to become the greatest mathematician since antiquity - while juggling sausages? In 1796 Gauss pub. the first proof of the Quadratic Reciprocity Theorem (Golden Theorem of Arithmetic), which allows the solvability of a quadratic equation in modular arithmetic to be determined without giving a method for finding it. In 1801 Gauss pub. Disquisitiones Arithmeticae, which founds the mathematical field of Number Theory, incl. the theory of congruences, quadratic forms, and quadratic residues.

In 1812 French mathematician-physicist-astronomer Jacques Philippe Marie Binet (1786-1856) discovers the rule for matrix multiplication, going on to lay the foundations of matrix algebra.

In 1813 French mathematician Simeon (Siméon) Denis Poisson (1781-1840) pub. Poisson's Equation, a generalization of Laplace's equation.

In 1821 French mathematician Baron Augustin-Louis Cauchy (1789-1857) pub. Cours d'Analyse, the first halfway decent correct mathematical definition of limit for Calculus purists, along with the first systematic study of convergence of series, the first theory of functions of a complex variable, and the definition of derivative and integral in terms of limits. In 1823 he rigorously proves the Fundamental Theorem of Calculus. He goes on to found complex analysis and the theory of permutation groups in abstract algebra, and pub. 800 articles and five textbooks.

In 1822 French mathematician Baron Jean-Baptiste Joseph Fourier (1768-1830) pub. On the Propagation of Heat in Solid Bodies (Theorie Analytique de la Chaleur), his mathematical theory of heat conduction, introducing his hot new Fourier Series, expansions of piecewise continuous functions as trigonometrical series. In 1825 he discovers the Greenhouse Effect.

In 1822 French mathematician Jean-Victor Poncelet (1788-1867) pub. Traite (Traité) des Proprietes (Propriétés) Projectives des Figures, a treatise on projective geometry, reviving the subject.

The modern Tower of Babel? In 1823 English mathematician Charles Babbage (1791-1871) invents the first working digital calculating machine, the Difference Engine to calculate tables of functions by finite difference methods. In 1833 he invents the Analytical Engine, the first large scale digital calculating machine (computer); he never gathers enough funds to build it; in 1991 it is built according to his specs, and works. In 1842-3 Augusta Ada King, Countess of Lovelace (1815-52), daughter of Lord Byron (1788-1824) tr. a memoir by Italian mathematician Federico Luigi, Count of Menabrea (1809-96) on the Analytical Engine of Charles Babbage, publishing the first known computer program, which calculates Bernoulli numbers; really written by Babbage?

In 1823 21-y.-o. Hungarian mathematician Janos (Johann) Bolyai (1802-60) and 30-y.-o. Russian mathematician Nikolai Ivanovich Lobachevsky (1792-1856) independently discover Non-Euclidean Geometry; the same year French mathematician Adrien-Marie Legendre (1752-1833) comes up with a bogus proof of Euclid's Fifth Postulate, stumbling over the big breakthrough without realizing it? On Oct. 25, 1733 Italian mathematician (Jesuit priest) Giovanni Girolamo Saccheri (b. 1667) dies after pub. Euclid Freed of Every Flaw (Euclides ab Omni Naevo Vindicatus), in which he reveals his discovery of non-Euclidean (hyperbolic) geometry, but doesn't realize it since he is trying to prove Euclid's parallel postulate true by a rudctio ad absurdum proof; 50 years later J.H. Lambert also stumbles over it, and 40 years after that (1823) Bolyai and Lobachevsky finally get the brain man brownie buttons; Saccheri's book also describes the Saccheri (Khayyam-Saccheri) Quadrilateral, which has two equal sides perpendicular to the base.

On May 31, 1832 French mathematician Evariste (Évariste) Galois (b. 1811) dies in Paris after a duel, leaving revolutionary papers giving necessary and sufficient conditions for the solution of equations by radicals using invariant (normal) subgroups, founding mathematical Group Theory; super-mathematician Gauss looks the stuff over and shrugs it off?

In 1837 German mathematician Johann Peter Gustav Lejeune Dirichlet (1805-59) pub. Dirichlet's Theorem on Arithmetic Progressions, that there are infinitely many primes that are congruent mod d, where a and d are positive and coprime, e.g. a, a+d, a+2d, a+3d..., using Dirichlet L-functions in the proof and describing the difference between absolute and conditional convergence of series, founding Analytic Number Theory; in 1829 he pub. a paper showing the conditions for the convergence of a Fourier series; in 1838-9 he pub. two papers proving the first class number formula for quadratic forms; he goes on to prove Dirichlet's Unit Theorem and Dirichlet's Approximation Theorem for Diophantine equations, define the Dirichlet Probability Distribution and the Dirichlet Process, and give the first modern definition of a function.

In 1838 French mathematician Antoine Augustin Cournot (1801-77) pub. Researches into the Mathematical Principles of the Theory of Wealth, which founds modern economic analysis, introducing functions and probability into economics, deriving the first equation for supply and demand as a function of price and becoming the first to graph supply-demand curves, and proposing the Cournot Duopoly (Competition) Model, where firms are free to set the amount of output they produce, proposing the concepts of Nash Equilibrium, Monetary Policy Reaction Function, and Best Response Dynamics.

In 1838 after reading Thomas Malthus' "An Essay on the Principle of Population" (1798), French mathematician Pierre Francois Verhulst (1804-49) pub. the Logistic Equation to model pop. growth; in 1925 Alfred J. Lotka renames it the Law of Pop. Growth.

On Oct. 16, 1843 after a decade of searching for a way to describe rotations in space, Irish mathematician Sir William Rowan Hamilton (1805-65) carves his discovery into the Broome Bridge in Dublin, then pub. the first description of Quaternions, an extension of complex numbers to 3 dimensions. In 1853 he pub. a paper stating the Cayley-Hamilton Theorem, that every square matrix over a commutative ring satisfies its own characteristic equation, which is refined in 1858 by Arthur Cayley. Hamilton's friend John Graves uses quaternions to create Octonions.

In 1843 French mathematician Adhemar Jean Claude Barre (Adhémar Jean Claude Barré) de Saint-Venant (1797-1886) pub. the first correct derivation of the Navier-Stokes Equations for viscous flow, and becomes the first to identify the coefficient of viscosity as the multiplying factor for velocity gradients in the flow; too bad, English physicist Sir George Gabriel Stokes (1809-1903) ends up getting credit after he asks his Cambridge students to solve it for prize exams in 1854, even though he got the solution in 1850 from Lord Kelvin.

In 1844 German polymath Hermann Gunther Grassmann (1809-77) pub. The Calculus of Linear Extension, A New Branch of Mathematics (Ausdehnungslehre), which founds linear algebra and develops the idea of a vector space; his mentor Mobius can't understand it, and he gets little credit, and rival mathematician Adhemar Jean Claude Barre de Saint-Venant claims to have developed his ideas first, causing him to switch to linguistics; 2nd revised ed. pub. in 1862.

In 1850 after obtaining his degree in 1845 under teachers Ernest Kummer and Peter Gustav Lejeune Dirichlet and quitting to manage a large farm and give his cousin-wife Fanny six children, German mathematician Leopold Kronecker (1823-91) launches his career with a paper solving the quintic equation via group theory, followed in 1853 by a paper extending the work of Evariste Galois, propsing the Kronecker-Weber Theorem sans proof (later given by David Hilbert), conjecturing Kronecker's Jugendtraum, which becomes Hilbert's Twelfth Problem (solved in ?); in 1855 he moves to Berlin 1855 and becomes friends with Karl Weierstrss, going on to introduce the Structure Theorem for Finitely-Generated Abelian Groups, the Theory of Divisors as an alternative to Dedekind's Theory of Ideals (which doesn't catch on), and propose the Kronecker Limit Formula, Kronecker's Congruence, the Kronecker Delta Function along with the Kronecker Cromb and the Kronecker Integral, the Kronecker Symbol (1885) (a generalization of the Jacobi Symbol to all integers), the Kronecker Matrix Product, the Kronecker Method for Factorization of Polynomials (1882), Kronecker Substitution, Kronecker's Theorem (1884) in number theory, Kronecker's Lemma, and Eistenstein-Kronecker Numbers; he also criticizes Gregor Cantor's work on set theory, which causes him to fall out with Weierstrass.

In 1850 English mathematician James Joseph Sylvester (1814-97) coins the term "matrix", followed by "graph", "discriminant", and "totient" for Euler's function psi, pioneering the development of matrix theory.

In 1851 French mathematician Joseph Liouville (1809-82) proves the existence of transcendental numbers, whose decimal expansions neither terminate nor repeat.

In 1851 the Thue-Morse Sequence, consisting of a series of bit strings recursively concatenated with their negations is first described by French mathematician Eugene (Eugène) Prouhet (1817-67).

In 1852 Russian mathematician ("Father of Russian Mathematics") Pafnuty Lvovich Chebyshev (1821-94) proves Chebyshev's Theorem, that the (n+1)th prime is less than 2 times the nth prime, leading to the Chevyshev Inequality, which is used to prove the Weak Law of Large Numbers; he goes on to develop Chevyshev polynomials and the Chebyshev bias; his students incl. Dmitry Grave, Alexander Korkin, Alexander Lyapunov, and Andrei Markov, spawning 10.5K by 2015.

In 1854 English mathematician George Boole (1815-64) of Queen's College in Cork, Ireland pub. An Investigation of the Laws of Thought, on Which Are Founded the Mathematical Theories of Logic and Probabilities, founding Boolean Algebra.

In 1854 Richmond, Surrey-born English mathematician Arthur Cayley (1821-95) pub. a paper proving Cayley's Theorem, that every group is isomorphic to a subgroup of the symmetric group acting on it, meaning that every group is a permutation group of some underlying set. He goes on to help found the modern British school of pure mathematics.

In 1858 German mathematician August Ferdinand Mobius (Möbius) (1790-1868) and German mathematician Johann Benedict Listing (1808-82) independently discover the Mobius (Möbius) Band (Strip); he doesn't pub. it until 1865 - after exhausting all the military possibilities?

In 1858 Conn.-born mathematician Elizur Wright (1804-85) reforms life insurance by getting a law passed in Mass. requiring insurance cos. to hold reserve funds based on a formula he discovered, becoming known as "the Father of Life Insurance and Insurance Regulation".

In Aug. 1859 German mathematician Georg Friedrich Bernhard Riemann (1826-66) makes his famous mathematical conjecture known as the Riemann Hypothesis at the Berlin Academy of Science, which is tied with the nature of prime numbers and makes John Nash and a zillion other math geeks spin their wheels all their lives trying to get a $1M prize: "All nontrivial zeroes of the Riemann Zeta Function have real parts equal to 1/2."

In 1860 English mathematician-logician Augustus De Morgan (1806-71) pub. Syllabus of a Proposed System of Logic, which founds Relation Algebra, which is used by Bertrand Russell and Alfred North Whithead in their "Principia Mathematica", and developed by Charles Sanders Peirce, Ernst Schroeder, and Alfred Tarski.

On Jan. 16, 1865 the London Mathematical Society is founded in London, England, with mathematician Augustus De Morgan as pres. #1. (until 1866).

In 1865 German mathematician Julius Plucker (1801-68) invents Plucker Coordinates - lucky plucker jokes here?

In 1865 Prussian-born German mathematician ("Father of Modern Analysis") Karl Weierstrass (1815-97) proves the Bolzano-Weierstrass Theorem, that every bounded infinite set of points in a Euclidean space has at least one accumulation point, for which every neighborhood of that point contains a point in the set; it was proved earlier by Austrian Roman Catholic priest-mathematician Bernhard (Bernardus Placidus Johann Nepomuk) Bolzano (1781-1848), so they share credit; the theorem along with the Intermediate Value Theorem (proved by Bolzano in 1817) and Weierstrass' definition of uniform convergence of a sequence of functions and his definition of a continuous function become the basis of the modern theory underlying mathematical limits, the unyummiest subject for college math students.

In 1871 St. Petersburg, Russia-born German mathematician Georg Ferdinand Ludwig Philipp Cantor (1845-1918) founds the Theory of Point Sets, then next year becomes a prof. at the U. of Halle, going on to develop the Theory of Transfinite Numbers, which are larger than all finite numbers, but not necessarily absolutely infinite. In 1873 he proves that the rational numbers are countable (can be put into 1-1 correspondence with the natural numbers), and that the real numbers are not - that would make them unreal, or does real mean not natural? In 1878 he proposes the Continuum Hypothesis, that there is no set whose cardinality is strictly between that of the integers and that of the real numbers, which his teacher Leopold Kronecker vehemently opposes, causing him to spend the rest of his life vainly trying to prove it, driving him insane. On Jan. 6, 1918 German "funky infinities" mathematician Georg Cantor (b. 1845) dies in a sanatorium after going mad trying to prove his 1878 Continuum Hypothesis; in 1940 Kurt Godel proves that it can't be disproven using the axioms of Zermelo-Fraenkel Set Theory, and in 1963 Paul Cohen proves that it can't be proven.

In 1872 German mathematician Richard (Julius Wilhelm Richar) Dedekind (1831-1916) rigorously defines irrational numbers arithmetically via the Dedekind Cut, a downward closed set without a greatest element, i.e., (-infinity, b) and [b, +infinity) - sounds like the coup de grace?

In 1872 Am. astronomer Asaph Hall (1829-2907) pub. an article on the experimental determination of pi by throwing a fine steel wire randomly onto a plane surface ruled with equidistant parallel lines, with pi being equal to 2 * (l/d) * (n/i), where l = length of wire, d = distance between lines, n = # of trials, and i = # of intersections.

In 1873 French mathematician Charles Hermite (1822-1901) proves that e is transcendental, i.e., not a root of any algebraic equation with rational coefficients.

In 1873 the value of pi is computed to 707 decimal places by William Shanks (1812-82) sans digital computers; too bad, it is only correct to 527 decimal places.

In 1877 English polymath Sir Francis Galton (1822-1911) (Charles Darwin's half-cousin) invents Statistical Regression toward the Mean.

In 1879 English "Alice in Wonderland" author Lewis Carroll (Charles Lutwidge Dodgson) (1832-98) pub. Euclid and his Rivals, which defends Euclid's Elements as the best textbook for geometry, dissing the Assoc. for the Improvement of Geometrical Teaching (founded 1871); he goes on to pub. 10+ books on recreational matehamatics, along with serious research on linear algebra, symbolic logic, probability, determinants, proposing Dodgson Condensation, and voting systems, proposing Dodgson's Method.

In 1882 German mathematician Carl Louis Ferdinand von Lindemann (1852-1939) proves that pi is transcendental (non-algebraic), i.e., not the root of any algebraic equation with rational coefficients, although, duh, irrational numbers such as the square root of 2 can be algebraic (solution of x^2 - 2 = 0).

In 1884 English theologian Edwin Abbott Abbott (1838-1926) pub. the novel Flatland: A Romance of Many Dimensions, in which A Square encounters a Sphere from another world; it is ignored until Einstein's Theory of Relativity comes out, after which it becomes a classic.

In 1888 German mathematician David Hilbert (1862-1943) pub. Hilbert's Basis Theorem, that a polynomial ring over a Noetherian ring is Noetherian, becoming the first "constructive proof", proving the existence of something without being able to display it, using the Law of the Excluded Middle (principium tertii exclusi) (tertium non datur) ("Either P or not P"), causing the ed. of Mathematische Annalen to comment: "This is not mathematics, this is theology", after which he adds "I have convinced myself that even theology has its merits"; the Intuitionist School of Mathematics ("the proof is the object") takes off with this idea and runs with it. In 1900 he announces Hilbert's 23 Unsolved Problems of Mathematics at the Internat. Congress of Mathematicians, which take the rest of the cent. to assimilate; meanwhile fellow German mathematician Friedrich Ludwig Gottlob Frege (1848-1925) disputes his whole approach, based on his 1884 book The Foundations of Arithmetic (Die Grundlagen der Arithmetik), which makes fans of Bertrand Russell and Ludwig Wittgenstein - Math is a Battlefield? In 1920 he proposes Hilbert's Program, an attempt to prove that all of mathematics follows from a finite set of axioms, and is consistent; too bad, Kurt Godel blows the program out of the water in 1931 with his Incompleteness Theorem. In 1970 Russian mathematician Yuri Vladimirovich Matiyasevich (1947-) proves that Hilbert's Tenth Problem (1900) is unsolvable.

In 1888 the Am. Mathematical Society (AMS) (originally New York Mathematical Society) is founded in New York City by Am. mathematician Thomas Scott Fiske (1865-1944) of Columbia U., going on to begin pub. Transactions of the Am. Mathematical Society in 1900, Proceedings of the Am. Mathematical Society in 1950, and Journal of the Am. Mathematical Society in 1988; in 1951 it moves its HQ to Providence, R.I.

In 1890 Italian mathematician Gregorio Ricci-Curbastro (1853-1925) invents Tensor (Absolute Differential) Calculus (Analysis), which uses contravariant (superscript) and covariant (subscript) array indices to represent physical objects independent of coordinate systems; in 1898 German physicist Woldemar Voigt (1850-1919) coins the term "tensor"; Ricci-Curbastro's student Tullio Levi-Civita (1873-1941) popularizes it in a 1900 textbook, and Albert Einstein later uses it in his Gen. Relativity Theory after taking 10 slow years to learn it, along with elliptic geometry from his friend Marcel Grossmann (1878-1936) - just move on up to relieve?

In 1895 French polymath mathematician-physicist ("the last Universalist" - Eric Temple Bell) Henri Jules Poincare (Poincaré) (1854-1912) pub. the paper Analysis Situs, defining Poincare Duality, proposing the Poincare Conjecture (solved in 2003), and founding Algebraic Topology, later applying it to celestial mechanics.

In 1896 Belgian mathematician Charles Jean Gustave Nicolas Baron de la Vallee Poussin (Charles-Jean Étienne Gustave Nicolas Le Vieux, Baron de la Vallée Poussi) (1866-1962) and French mathematician Jacques-Salomon Hadamard (1865-1963) independently prove the Prime Number Theorem, that all natural numbers are the product of one or more primes.

In 1899 Austrian mathematician Georg Alexander Pick (1859-1942) pub. the cool Pick's Theorem, giving the area of a simple lattice polygon as the number of interior points plus half the number of boundary points minus 1 for burgers.

In 1900 French mathematician Henri Leon Lebesgue (1875-1941) formulates the Mathematical Theory of Measure, followed by the Lebesgue Integral (1902-4).

In 1906 Russian mathematician Andrei (Andrey) Andreyevich Markov (Markoff) (1856-1922) pub. a paper describing the Markov Chain, a stochastic process in which one may predict the next value of a squence based on the last state alone.

In 1906 and 1909 Finnish mathematician Karl Frithiof Sundman (1873-1949) proves the existence of a convergent infinite series solution to the three-body problem, which is generalized to more than three bodies in 1991 by Qiudong Wang at the U. of Ariz.

In 1907 Goodwater, Ala.-born mathematician Robert Daniel Carmichael (1879-1967) proposes Carmichael's Totient Function Conjecture, producihg a faulty proof that he withdraws in 1922; it is first solved in ?; "A thing is obvious mathematially after you see it"; "He who discovers a fact or makes known a new law or adds a novel beauty to truth in any way makes every one us his debtor. How beautiful upon the highway are the feet of him who comes bringing in his hands the gift of a new truth to mankind."

In 1909 Danish mathematician Agner Krarup Erlang (1878-1929) pub. "The Theory of Probabilities and Telephone Conversations" to describe probabilities of equipment use in the Copenhagen telephone exchange, founding Queueing Theory; he follows it in 1917 with "Solution of Some Problems in the Theory of Probabilities of Significance in Automatic Telephone Exchanges".

In 1909 French mathematician Marie Ennemond Camille Jordan (1838-19220 pub. Cours d'analyse de l'Ecole Polytechnique (3 vols.), which becomes a std. textbook. He goes on to bring Galois Theory into the mainstream, investigate Mathieu Groups (first known sporadic groups), and pub. the Jordan Curve Theorem, Jordan Normal Form, Jordan (Peano-Jordan) Measure (Content), Jordan-Holder Theorem on Composition Series, and the Jordan-Schurch Theorem on Finite Linear Groups.

In 1910-13 British mathematician-philosophers Bertrand Athur William Russell, 3rd Earl Russell (1872-1970) and Alfred North Whitehead (1861-1947) pub. Principia Mathematica, which attempts to reduce arithmetic to logic, founding the calculus of propositions and modern symbolic logic, becoming king locomotive of the county until Godel's Theorem derails them?

In 1912 Italian mathematical statistician Corrado Gini (1884-1965) pub. the paper "Variability and Mutability", defining the Gini Coefficient, which is later used as a measure of inequality of income or wealth distribution, as well as biodiversity, with a 0 value indicating a perfectly equal distribution, and a 1 value a perfectly unequal distribution (one individual has it all); too bad, Gini later stinks his name up by claiming to scientifically back up Fascism.

On Jan. 16, 1913 self-taught Indian mathematician Srinivasa Iyengar Ramanujan (1887-1920) writes to English mathematician Godfrey Harold "G.H." Hardy (1877-1947), wowing him with lists of unknown theorems, "the one romantic incident in my life" (Hardy), deciding that they "must be true, because if they were not true, no one would have the imagination to invent them", bringing him from Madras to Cambridge in 1914, getting elected a fellow of Trinity College on Oct. 13, 1918; too bad, he returns to Madras in 1919, and dies of TB (amoebiasis?) on Apr. 26, 1920; in 1911 Hardy begins a collaboration with English mathematician John Edensor Littlewood (1885-1977) leading English mathematicians away from applied math a la Isaac Newton to the Continental rigorous theoretical type; on July 10, 1908 Hardy pub. Mendelian Proportions in a Mixed Population, announcing the Hardy-Weinberg Principle that allele and genotype frequencies in a breeding pop. remain constant over generations unless disturbed by evolutionary influences incl. mate choice, mutation, selection, genetic drift, gene flow and meiotic drive; in 1940 Hardy pub. his autobio. A Mathematician's Apology, which laments the passing of his creative powers; "I believe that mathematical reality lies outside us, that our function is to discover or observe it, and that the theorems which we prove, and which we describe grandiloquently as our 'creations', are simply the notes of our observations" (Hardy); "I read in the proof sheets of Hardy on Ramanujan: 'As someone said, each of the positive integers was one of his personal friends.' My reaction was, 'I Wonder who said that; I wish I had." (Littlewood); "Before creation, God did just pure mathematics. Then He thought it would be a pleasant change to do some applied." (Littlewood)

In 1915 Polish mathematician Waclaw Franciszek Sierpinski (1882-1969) pub. the Sierpinski Triangle (Gasket) (Sieve), followed next year by the Sierpinski Carpet plane fractal universal curve, going on to generalize it as the Sierpinski Curve; he also invents the Sierpinski Number.

In 1918 East Finchley, London, England-born geneticist-statistician-eugenicist Sir Ronald Aylmer Fisher (1890-1962) pub. the paper The Correlation between Relatives on the Supposition of Mendelian Inheritance, proposing the Infinitesimal (Polygenic) Model of genetics, in which continuous variation of phenotypic traits could be the result of Mendelian inheritance among an infinitely large number of genes that each make an infinitely small contribution to the phenotype (not excluding environmental factors), coining the statistical term "variance" and becoming the first step toward establishing pop. genetics and quantitative genetics, reconciling the discontinuous nature of natural selection with gradual evolution; it contains the soundbyte that if a trait is polygenic, "the random sampling of alleles at each gene produces a continuous, normally distributed phenotype in the population." In 1924 Fisher pub. the paper "On a distribution yielding the error functions of several well known statistics", starting with the Gaussian distribution and progressing through Pearson's chi-squared test and William Gosset's Student's t-distribution to his own F-distribution. In 1925 Fisher pub. Statistical Methods for Research Workers (14th ed. 1970), which becomes a std. textbook, explaining Fisher's method for data fusion along with the p-value, with the soundbyte: "The value for which P = 0.05, or 1 in 20, is 1.96 or nearly 2 ; it is convenient to take this point as a limit in judging whether a deviation is to be considered significant or not." In 1930 Fisher pub. The Genetical Theory of Natural Selection, reviving Charles Darwin's idea of sexual selection and founding Population Genetics. In 1935 Fisher pub. The Design of Experiments, introducing the concept of the null hypothesis in the Lady Tasting Tea Experiment. In 1936 Fisher analyzes Gregor Mendel's data using the Pearson's chi-squared test, concluding that the predicted ratios were too perfect, implying fiddling with the data. In 1936 Fisher founds Discrimination Analysis, introducing the Iris Flower Data Set. In 1937 he pub. the paper "The wave of advance of advantageous genes", proposing Fisher's Equation to describe the spatial spread of an advantageous allele, advancing pop. genetics. "Natural selection is a mechanism for generating an exceedingly high degree of improbability."

In 1920 Polish mathematician Stefan Banach (1892-1945) introduces the concept of Banach Space, founding modern Functional Analysis.

In 1920 Am. mathematician Edward Kasner (1878-1955) coins the word "Google" to mean 1 followed by 100 zeroes (ten duotrigintillion); the name was thought up by his 9-y.-o. nephew Milton Sirotta (1911-81). In 1940 he and James Roy Newman (1907-66) pub. Mathematics and the Imagination, which introduces the term googol, and claims that it would take a human 10 years of calculation to compute the value of pi to 1K places.

In 1920 Polish mathematician Jan Lukasiewicz (1878-1956) invents Polish (Lukasiewicz) (Warsaw) (Prefix) Notation, which dispenses with parentheses and places operators before operands to make for unambiguous parsing, becoming popular with computer scientists, who use it with a last-in first-out recursive stack computer memory.

In 1921 French mathematician Felix Edouard Justin Emile (Félix Édouard Justin Émile) Borel (1871-1956) begins pub. a series of papers on Game Theory, becoming the first to define games of strategy. In 1928 Budapest, Hungary-born Am. mathematician John von Neumann (1903-57) pub. On the Theory of Parlor Games, announcing the Minimax Theorem; "As far as I can see, there could be no theory of games... without that theorem... I thought there was nothing worth publishing until the Minimax Theorem was proved." In 1944 von Neumann and Gorlitz, Germany-born Austrian School economist Oskar Morgenstern (1902-77) pub. Theory of Games and Economic Behavior, which treats cooperative multiplayer games with decision-making under uncertainty, founding Mathematical Game Theory. Borel goes on to pioneer measure theory and its application to probability theory, incl. the Borel Set, and propose the Infinite Monkey Theorem in 1913.

In 1931 Am. mathematician George David Birkhoff (1884-1944) proposes the Ergodic Theorem, that an individual particle will go through all the states seen in an infinite pop. at an instant in time.

In 1931 Brunn, Austria-born mathematical logician Kurt Friedrich Godel (Gödel) (1906-78) pub. the paper On Formally Undecidable Propositions in 'Principia Mathematica' and Related Systems I, showing that in any axiomatic mathematical system there are propositions that cannot be proved or disproved within the axioms of the system, because a Godel numbering scheme can be devised which allows the proposition to be constructed that "This theorem is false", which is like when Capt. Kirk talks the computer into blowing itself up?; the paper proves to be so good that he decides against a "II".

One World Government fans watch with glee as the citizens of the U.S. are robbed by their own government, while the citizens of Germany are robbed of brainpower by theirs? On Apr. 5, 1933 U.S. Pres. Roosevelt commands all U.S. citizens to surrender their gold to the govt. at just $20.67 an oz. or face a 10-year prison sentence, then later devalues the dollar 40% by raising the price of gold to $35 an oz.; on Apr. 19 the U.S. goes off the gold standard; 445.5K golden Double Eagle coins minted this year are withheld from circulation and melted down, but a handful survive and become some of the most sought-after coins by collectors; on June 5 Congress voids all gold clauses in public and private debts. On Apr. 7 Nazi Germany passes a law banning Jews from civil service jobs (except if they served Germany in WWI), forcing Jewish professors out, ruining Gottingen U.'s math dept. et al., and ending Germany's supremacy in science; when Nazi education minister Bernhard Rust asks David Hilbert "How is mathematics at Gottingen, now that it is free of the Jewish influence?", he replies "There is no mathematics in Gottingen anymore."

In 1934 Russian mathematician Alexander Osipovich Gelfond (1906-68) and German mathematician Theodor Schneider (1911-88) independently prove the Gelfond-Schneider Theorem, that an algebraic number to the power of an algebraic irrational number is transcendental, e.g., 2 to the power of the square root of 2 (the Gelfond-Schneider Constant), finally providing an infinite number of funky transcendental numbers to play with and answering Hilbert's Seventh Problem (1900) affirmatively; e to the pi power, known as Gelfond's Constant is also transcendental, and since it comes out to 23.14069... that proves that The Number 23 is the Answer to Life, the Universe, and Everything?

In 1935 Nicolas Bourbaki (pseudonym of a group of French mathematicians) begins pub. the first of a series of Works on Modern Mathematics, with the goal of grounding all of mathematics on set theory.

In 1936 the quadrennial Fields Medal is established by the Internat. Congress of Mathematicians for the most outstanding math achievement as an equivalent to the Nobel Prize; the first medal is awarded to Lars Valerian Ahlfors (1907-96) of Harvard U. and Jesse Douglas (1897-1965) of MIT (student of Edward Kasner); in 1953 Ahlfors pub. Complex Analysis, which becomes a std. text.

In 1936 British zoologist and statistician Lancelot Thomas Hogben (1895-1975) pub. the bestseller Mathematics For the Million: How to Master the Magic of Numbers.

In 1937 Scottish-born Am. mathematician Eric Temple Bell (1883-1960) pub. the bestseller Men of Mathematics: The Lives and Achievements of the Great Mathematicians from Zeno to Poincare, which covers 40+ mathematicians, making fans of Freeman Dyson, John Forbes Nash Jr., TLW et al.; too bad, it's full of moose hockey and anecdotal accounts? - TLW's favorite teenie nonfiction read?

In 1937 English mathematician Alan Mathison Turing (1912-54) pub. a paper on "computable numbers", discussing his invention of the Turing Machine, the theoretical precursor of the digital computer, and demonstrating the unsolvability of the halting problem.

In 1939 Soviet mathematician-economist Leonid Vitaliyevich Kantorovich (1912-86) invents Linear Programming for the optimal allocation of resources, receiving the 1975 Nobel Econ. Prize; Linear Programming is kept secret until 1947, the same year that Portland, Ore-born mathematician George Bernard Dantzig (1914-2005) pub. the Simplex Method, and Budapest, Hungary-born Am. mathematician John von Neumann (1903-57) pub. the theory of Duality. On June 30, 1945 John von Neumann et al. pub. the First Draft of a Report on the EDVAC, describing the Von Neuman (Princeton) Architecture for a Digital Computer, the first pub. description of a stored-program computer, which uses a single bus for the instruction fetch and the data operation, contrasting with the Harvard Architecture for a Digital Computer, which uses two or more buses, first proposed by Howard Hathaway Aiken (1900-73) in Nov. 1937 and used in the Harvard Mark I Computer in 1944.

In 1939 French mathematician Paul Pierre Levy (Lévy) (1886-1971) introduces the concept of Martingales into probability theory, where the expectation of the next value in a sequence is the present observed value, modeling fair games.

In 1940 French mathematician Andre (André) Weil (1906-98) pub. the Weil Conjectures about the generating (local zeta) functions derived from counting the number of points on algebraic varieties over finite fields, which aren't answered until 1974.

In 1948 Am. mathematician Claude Elwood Shannon (1916-2001) pub. the paper "Communication Theory of Secrecy Systems", founding modern cryptography; he also pub. A Mathematical Theory of Communication, which becomes the Magna Charta of the Information Age.

In 1948 Columbia, Mo.-born mathematician Norbert Wiener (1894-1964) pub. Cybernetics; or, Control and Communication in the Animal and Machine, defining Cybernetics (Gr. "steer", "navigate") as "the scientific study of control and communication in the animal and the machine", anticipating the Computer Rev. His Anselmo, Neb.-born student Jay Wright Forrester (1918-) founds System Dynamics. His Vienna, Austria-born student Heinz von Foerster (1911-2002) comes up with the Doomsday Equation, predicting that world. pop. will become infinite on Nov. 13, 2026 (Fri.); the Soviet Union bans the book until the death of Joseph Stalin on Mar. 5, 1953, then does a 180 and begins embracing computers.

In 1950 Am. mathematician Richard Wesley Hamming (1915-98) pub. a paper introducing the concept of Hamming Distance, allowing error-correcting codes to be created.

In Sept. 1951 Bluefield, W. Va. -born mathematician John Forbes Nash Jr. (1928-2015) pub. the article Non-Cooperative Games in The Annals of Mathematics, becoming the first to define a Nash Equilibrium for non-zero-sum games, winning a share of the 1994 Nobel Econ. Prize.

On Jan. 6, 1954 German-born mathematician Hans Peter Luhn (1896-1964) of IBM files a patent for the mod 10 Luhn Algorithm (ISO/IEC 7812-1), a mathematical formula for a checksum digit that corrects almost all single-digit errors; the patent is granted on Aug. 23, 1960, and ends up being used on credit cards after the patent expires; Luhn goes on to create the KWIC (Key Words In Context) indexing system.

In 1956 Am. computer scientists Allen Newell (1927-92) and Herbert Alexander Simon (1916-2001) develop the Logic Theory Machine (Logic Theorist), the first artificial intelligence (AI) program, which proves 38 of the first 52 theorems of Bertrand Russell and Albert North Whitehead's "Principia Mathematica", followed next year by the academically useful but practically useless Gen. Problem Solver (GPS), using the Info. Processing Language (IPL) - it's alive, weird science?

In 1963 Am. mathematician Paul Joseph Cohen (1934-2007) answers the first of the 23 famous problems of David Hilbert of 1900, proving that the negation of the 1870s Cantor's Continuum Hypothesis is consistent with classical (Zermelo-Fraenkel) set theory, proving the independence of the Axiom of Choice and the Continuum Hypothesis from Zermelo-Fraenkel Set Theory using his new technique of Forcing, winning him the Fields Medal in 1966, becoming the first awarded for mathematical logic (until ?); Kurt Godel already proved in 1938 that the hypothesis itself is consistent with classical set theory; thus, there are two types of mathematics possible, one that claims the hypothesis is true and another that says it is false, freaking out philosophers with the revelation that math can neither prove nor disprove well-known concrete mathematical assertions - hey sugarfoot, how do you like your new home?

In 1963 after his 12-variable computer weather model gives grossly different weather patterns depending on minute variations in the initial values of the variables, Am. mathematician Edward Norton "Ed" Lorenz (1917-2008) pub. the paper Deterministic Nonperiodic Flow, in which he describes the Lorenz Attractor, and coins the term Butterfly Effect, issuing the soundbyte: "One meteorologist remarked that if the theory were correct, one flap of a seagull's wings could change the course of weather forever", with Ray Bradbury's butterfly (from a 1952 short story) later substituted, becoming the beginning of Chaos Theory, the behavior of dynamical systems that are highly sensitive to initial conditions; unsung heroines Ellen Fetter and Margaret Hamilton program the big clunky Royal McBee LGP-30 computer for him at MIT. In 1987 James Gleick pub. Chaos: Making a New Science, which introduces the Chaos Theory of Edward Norton Lorenz to the public.

In 1964 Finnish mathematician Lars Valerian Ahlfors (1907-96) pub. the proof of the Ahlfors Finiteness Theorem for Kleinian groups.

In 1965 Austrian math student Bruno Buchberger (1942-) develops the theory of Grobner (Gröbner) Bases for polynomial rings, named after his adviser Wolfgang Grobner (Gröbner) (1899-1980), which become important for computer algebra and integer programming, and finally provide an example to go with David Hilbert's "theological" 1888 Basis Theorem.

In 1965 Am. mathematicians James William Cooley (1926-) and John Wilder Tukey (1915-2000) discover the cool Cooley-Tukey Fast Fourier Transform (FFT) (Butterfly) Algorithm for computers, radically speeding up the calculation of Fourier Transforms and permitting real-time computer spectral analysis; it was actually discovered in 1805 by German mathematician Carl Friedrich Gauss; the FFT becomes the most important computer algorithm of the 20th cent.; in 1983 Australian-born electrical engineer Ronald Newbold Bracewell (1921-2007) of Stanford U. discovers the Fast Hartley-Bracewell Algorithm that can replace the Fast Fourier Transform (FFT).

In 1965 British Jewish mathematician Irving John Good (Isadore Jacob Gudak) (1916-2009) pub. the papers "Speculations Concerning the First Ultraintelligent Machine" and "Logic of Man and Machine", in which he proposes a future "intelligence explosion" when smart machines will begin designing even more intelligent machines, eventually leaving the human race behind in the "technological singularity"; he is hired by Stanley Kubrick as a consultant for his 1968 film "2001: A Space Odyssey"; "Let an ultraintelligent machine be defined as a machine that can far surpass all the intellectual activities of any man however clever. Since the design of machines is one of these intellectual activities, an ultraintelligent machine could design even better machines; there would then unquestionably be an 'intelligence explosion,' and the intelligence of man would be left far behind. Thus the first ultraintelligent machine is the last invention that man need ever make" - Adam and Eve already heard that one?

In 1967 Canadian-born Princeton U. math. prof. Robert Phelan Langlands (1936-) proposes the Langlands Program in a letter to mathematician Andre Weil, followed by the 1970 book "Problems in the Theory of Automorphic Forms", a grand attempt to unify mathematics, which goes on to establish connections between number theory and harmonic analysis (Galois groups, representation theory, and automorphic forms), and allows British mathematician Andrew Wiles to solve Fermat's last theorem.

In 1967 Chicago, Ill.-born mathematician Edward Oakley Thorp (1932-) pub. the book Beat the Dealer: A Winning Strategy for the Game of Twenty-One, the first book to advocate card counting in blackjack.

In 1968 French mathematician Rene Frederic (René Frédéric) Thom (1923-2002) pub. the first paper describing Catastrophe Theory - good timing considering the Paris riots?

In 1968 Italian physicist Gabriele Veneziano (1942-) of CERN discovers that the physics of the strong nuclear force can be modeled by Euler's Gamma Function, which he finds in a book on the history of mathematics by chance, becoming the beginnings of Superstring Theory.

In 1968 Carl Engleman (1938-83), William A. Martin (1938-81), and Joel Moses (1941-) of MIT develop Macsyma-1, the first computer algebra system, performing 600+ types of mathematical operations, hosted on a PDP-6; it is put on the Arpanet, continuing development until 1982; it was originally (1964) called Mitre, then MATHLAB 68.

In 1970 Russian mathematician Yuri Vladimirovich Matiyasevich (1947-) proves that Hilbert's Tenth Problem (1900) is unsolvable.

In 1972 UCB asst. math prof. Stephen Arthur Cook (1939-) proves that the Boolean Satisfiability Problem in formal logic is NP-Complete, solvable in nondeterministic polynomial time; too bad, he leaves open the question of whether complexity classes P (solvable in polynomial time) and NP (solvable in nondeterministic polynomial time) are equivalent, and the math dept. at UCB stinks itself up by refusing to give him tenure, after which he moves to the U. of Toronto.

In 1973 Canadian computer scientists Brian Wilson Kernighan (1942-) and Shen Lin find a useful algorithm for solving the classic Traveling Salesman Problem.

In 1974 Am. mathematicians Theodore P. Baker, John T. Gill III, and Robert Martin Solovay (1938-) demonstrate two classes of propositions which are equivalent based on one set of postulates but not equivalent based on another set, even though each postulate set is internally consistent - no way to solvy?

In 1974 Belgian mathematician Pierre Rene (René) Deligne (1944-) resolves three of Andre Weil's 1949 conjectures about using algebraic geometry, becoming the first mathematician in history to be commemorated on a postage stamp during his lifetime (until ?).

In 1974 English mathematician Sir Roger Penrose (1931-) discovers Penrose Tiling of a plane using fat and thin rhombuses such that their ratio is an irrational number, the Golden Mean.

In 1974 German historian Arno Peters (1916-2002) discovers the Arno (Gall-Peters) Projection, which turns out to have been devised in 1855 by Scottish clergyman James Gall (1808-95), which retains the proportions of countries better than the Mercator and Van der Grinten map projections, and has the political effect of giving Third World countries a bigger presence.

In 1975 Am. mathematical physicist Mitchell Jay Feigenbaum (1944-) discovers the First Feigenbaum Constant (4.669201609103+), the ratio toward which the consecutive differences of almost any iterated function tends; in 1978 he discovers the 2nd constant.

In 1975 the term "fractal" is coined by Polish-born French-Am. mathematician Benoit B. Mandelbrot (1924-2010), who founds Fractal (Expanding or Evolving Symmetry) Geometry; in 1979 he discovers the Mandelbrot Set.

In 1976 Am. mathematician Kenneth Ira Appel (1932-) and German mathematician Wolfgang Haken (1928-) solve the famous 4-Color Map Theorem, that four colors can color any planar map; too bad, they used a computer to number-crunch the possibilities, pissing-off some mathematicians while founding the new field of Experimental Mathematics.

In 1976 Am. mathematicians Bailey Whitfield "Whit" Diffie (1944-) and Martin Edward Hellman (1945-) pub. the paper "New Directions in Cryptography", introducing the Diffie-Hellman Key Exchange Algorithm for public-key cryptography; in 2002 the name of Ralph C. Merkle (1952-) is added.

In 1979 Am. mathematicians Robert Stephen "Bob" Boyer and J [no period] Strother Moore, developers in 1977 of the efficient Boyer-Moore String Search Algorithm develop the Boyer-Moore Theorem Prover Algorithm, which can churn out proofs by mathematical induction on a computer.

In 1979 Harvard dropout Microsoft founder William Henry "Bill" Gates III (1955-) pub. his first (only) mathematical paper, "Bounds for Sorting by Prefix Reversal", on the Pancake Flipping (Sorting) Problem.

In 1981 Cleveland, Ohio-born mathematician Karen Keskulla Uhlenbeck (1942-) pub. the paper "The existence of minimal inversions of 2-spheres" with Jonathan Sacks, helping found the field of geometric analysis, the use of differential geometry to study the solutions to differential equations, and vice-versa. In 1983 she follows with the paper "Closed minimal surfaces in hyperbolic 3-manifolds". In 2019 she becomes the first woman to win the Abel Prize since its 2003 inception.

In 1982 Brazilian mathematics grad student Celso Costa (1949-) discovers Costa's Minimal Surface, a thrice-punctured torus which mathematically describes the first new non-self-intersecting (embedded) minimal surface in over a cent.; James Hoffman of the U. of Mass. generates computer pictures proving him right - is that a 3 or 4-sheeter?

In 1983 Am. mathematicians Leonard Max Adelman (1945-), Carl Bernard Pomerance (1944-), and Robert Scott Rumely (1952-) of USC pub. the Adelman-Pomerance_Rumely Primality Test, an improved computer test for prime numbers, which is later improved by Henri Cohen and Hendrik Willem Lenstra; in 1994 Adelman uses DNA in a test tube to solve a simple 7-node mathematical problem, making DNA Computers a possibility.

In 1983 British mathematician Howell Peregrine (1938-2007) discovers the Peregrine Soliton, a new nonlinear entity that may explain the formation of rogue waves in hydrodynamics that appear out of nowhere and disappear without a trace, and which becomes the defining object of nonlinear science; it takes until 2010 (3 years after his death) for the first physical example of it to be observed.

In 1987 English-born Am. mathematician Stephen Wolfram (1959-) founds Wolfram Research Inc., releasing Mathematica software algebra system for solving complex problems on June 23, 1988; in 2002 he pub. A New Kind of Science, which claims that simple programs not formulas are needed to do science because the Universe is ultimately digital.

In 1994 applied mathematician Peter Williston Shor (1959-) of MIT invents Shor's Algorithm to factor large numbers in polynomial time (log N) using a quantum computer, making the cracking of the RSA public-key cryptography scheme possible in theory, causing the govt. and computer users to get a little nervous; in 2009 a silicon chip that implements Shor's Algorithm is demonstrated by the U. of Bristol.

In 1994 English mathematician Sir Andrew John Wiles (1953-) finally proves Fermat's Last Theorem (1637) after seven years locked up by himself, and also proves that all rational semistable elliptic curves are modular.

On Dec. 21, 2001 Ron Howard's A Beautiful Mind (Imagine Entertainment) (Universal Pictures) debuts, based on the 1998 book by Sylvia Nasar, starring Russell Crowe as schizophrenic Princeton U. mathematician John Nash, who marries student Alicia (Jennifer Connelly) and fakes it for years until he is found out, which doesn't stop him from winning the 1994 Nobel Econ. Prize for helping invent game theory; features Ed Harris as imaginary secret agent William Parcher, Paul Bettany as imaginary friend Charles Herman; does $313M box office on a $58M budget; "Perhaps it is good to have a beautiful mind, but a greater gift is to discover a beautiful heart."

In Mar. 2008 Avraham Trakhtman, a Russian immigrant to Israel who worked as a night watchman becomes a real-life Good Will Hunting by solving the 1970 Road Coloring Problem, proving the existence of a universal map permitting a traveler to reach a given destination whatever his starting point.

In Oct. 2010 Gary Miller et al. of Carnegie Mellon U. announce a breakthrough algorithm for solving systems of linear equations that promises a revolution in image processing, logistics and scheduling problems et al.

On Jan. 21, 2011 Am. mathematician Ken Ono of Emory U. pub. a paper solving the age-old problem of partition numbers in number theory, proving that they behave like fractals.

On Apr. 17, 2013 Chinese-born Am. mathematician (former Subway sandwich shop worker) Yitang "Tom" Zhang submits a paper to Annals of Mathematics, which is pub. a record three weeks later, announcing a breakthrough in prime number theory by proving that there are infinitely many prime number pairs differing by less than 70M, helping close in on the Twin Prime Conjecture that there are infinitely many differing by 2.

On July 29, 2013 Amit Sahai et al. of UCLA pub. a Mathematical Jigsaw Algorithm to encrypt software so that someone can use it without being able to uncover the code behind it.

On Jan. 9, 2017 Michael Bowling et al. pub. an article in Science announcing the first perfect computer algorithm for solving heads-up limit hold'em poker.